Construction is not a new topic for us, we have been learning how to use a compass and other measuring tools to construct different shapes and angles. In class 10 maths chapter 11 constructions we will get in detail how we can divide a line segment in a given ratio using a compass, construct a triangle or similar triangle, and most importantly we will learn how to construct tangents of a circle and circle itself.
As you have studied in the previous class that a true geometrical construction is a process of drawing figures using only an ungraduated ruler (also known as straight edge) and a compass. When we use only these two tools, then only it can be said that we have constructed a real geometrical figure. And this is exactly what we will be doing in chapter 11 of class 10 i.e constructions.
Class 10 Maths Chapter 11 Constructions
If you are a regular user of this website, then you know that we have a tradition of going through the important terms and concepts that we have learned about the topic in earlier classes. And in this chapter also we will follow that trend and go through the important points that we had learned in class 9th.
In the previous class we learned:
- How we can bisect a given angle.
- How to draw the perpendicular bisector of a given line segment.
- How to construct an angle of 60° and other specific angles.
- How to construct a triangle when its base, base angle, and the sum of the other two sides are given.
- How to construct a triangle when its base, base angle, and the difference of the other two
sides are given. - How to construct a triangle when we are given its perimeter and two base angles.
So, we learned all this with a proper step-by-step guide. In case if you are still not able to remember all this, then it is suggested that you go through the NCERT book of class 9th at least once to refresh your memory, otherwise, you will not understand this chapter properly.
Class 10 Maths Chapter 11 Constructions
After refreshing the old topics, we are now ready to proceed to understand this chapter in detail. For this chapter there are is no theory to explain, therefore, we will directly go on with the constructions of this chapter.
# Division of a line segment
Objective: To divide a line segment in a given ratio.
Given: A line segment AB
We will divide the line segment in the ratio m:n (m and n are both positive integers). Lets assume that m = 3 and n = 2. Following are to steps to construct this line segment.
Step 1: Draw a line AX, making an acute angle with AB. (the angle can be made upwards or downwards)
Step 2: This step will be completed with the following substeps:
- Add the given ratios (m+n). In our case, we have 3+2=5. We will need to mark 5 points on the line AX at an equal distance.
- Now we will open our compass as much as we want and from point ‘A’, we will mark a point on the line AX and name it
. Make sure not to adjust the compass throughout this step. - Without adjusting the compass, from we will mark another point
on AX. And repeat this step till we mark all 5 points.
After completing this step we will get 
.
Step 3: Now, we will join point B (of line AB) to the point 
(of line AX). This will give us a line 
.
Step 4: The next step is to draw a parallel line to on our construction. This step will be also be achieved with the following substeps:
- From point we will mark an arc with the help of the compass making it an angle (
) of the triangle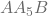 
. Note that it does not matter how much we open the compass. Do not adjust the compass after making the arc. - Without adjusting the compass, we will bring it to point
and mark an arc such that it touches the line AX. If you are using different ratios than us, then you will mark this arc on the point that corresponds to the value of ‘m’. Our value for ‘m’ is 3, therefore, the arc is made on . - Next, with the compass, we will measure the angle from the point where it touches the line AX to the point where it touches the line .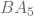
- Without adjusting the compass, We will place it at the point on arc (that we made on ) where it touches the line AX, and mark another arc such that both the arc intersects each other.
- Finally, we will draw a line passing through the point of intersection of both the arc that we just created such that it connects (value of ratio ‘m’) and the line AB. Let’s name the point (where this line will touch AB) as ‘C’. So, this will give us a line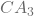
which will be parallel to the line .
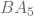Class 10 Maths Chapter 11 Constructions
This chapter also teaches how we can construct triangles, but will not discuss it as we have already learned a lot about it in previous classes. We will directly jump on how we can construct a tangent to a circle.
# Construction of tangents to a circle
Objective: To construct the tangents to a circle from a point outside it.
Given: There is a circle with center O and a point P outside it.
Step 1: Firstly, let’s join the points P and O to make it a line OP. Now let’s bisect this line meaning divide the line into two equal parts, and name the midpoint M.
Step 2. We will now draw a circle of radius that we will get by measuring the distance between M and O. Now, when we will draw this circle, then it will intersect the given circle. Let the points of intersection be Q and R.
Step 3: For the final part, just join PQ and PR and these are the two tangents of the given circle.
So, these are the two constructions that are illustrated in class 10 maths chapter 11 construction.
Leave a Reply